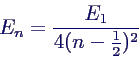
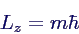
The eigenfunctions of the two-dimensional Coulomb potential are characterised by two quantum numbers:
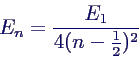
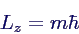
Study the eigenfunctions for different n amd m. Can the quantum numbers be identified using the graphical representation? You can change the central charge Z to zoom in and out.
If you start the time evolution, the absolute value image shouldn't move at all, while the real and imaginary parts should rotate with constant frequency. Unfortunately one easily runs into numerical problems here: If the function extends to the border, one gets boundary reflections; if it extends into the center, all kinds of artefacts show up, since the grid is too coarse to properly cope with the steep 1/r potential near the center.