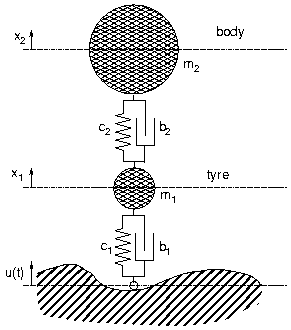

A simple model of the vertical vibrations of a car is the "Quarter Car", which consists of one mass for the car and a smaller mass for the tyre that is connected elastically to the car and the ground. Driving on uneven ground leads to excitations of the system that are here modelled by a harmonic function for the base point position u(t)
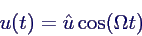
Besides the excitations xi(t) one is mainly interested in the vertical acceleration a2 of the car (and the driver) and in the total force R that is transmitted to the ground.
Use the applet to find for fixed car parameters the excitation frequencies where a2 or R are maximal. Then change the suspension parameters ci, bi to minimize either a2 or R. How could one define an "optimal" suspension system?
Use the standard procedures of vibration theory to verify your findings.