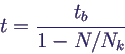Population models

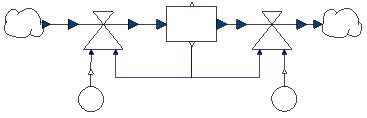
• Basic model:
  • stock describes size N of population
  • number of births and deaths proportional to N
    • G = g N
      T = t N
  • rates g, t in ConstantConverter blocks
  • products with Mult2Flow blocks
  • model population1
    • 
  • start with N(0) = 10
  • result for g = 0.03, t = 0.01: exponential growth
• Limited growth:
  • scarcity of resources → death rate grows for large population
  • approach: death rate proportional to N
    • t = (N/N_b) t_b
  • implement equation with MultPower3Converter
    • out = in1^k1 * in2^k2 * in3^k3
    • N: in1 = stock.out1, k1 = 1
    • t_b: in2 = 0.01 (coming from ConstantConverter), k2 = 1
    • N_b: in3 = 50 (coming from ConstantConverter), k3 = -1
  • complete model population2
    • 
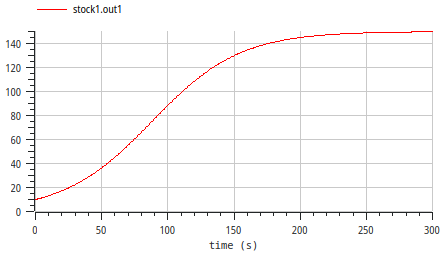
  • result
    • change plot range with plot setup to [0, 150]
    • 
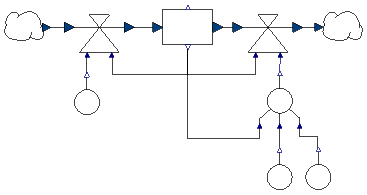
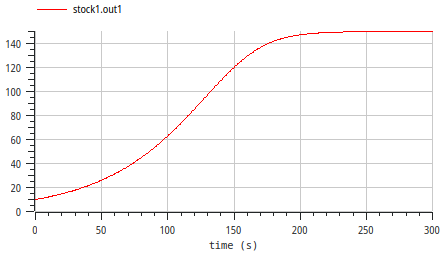
• Fixed capacity:
  • changes in population3
    • death rate stays constant for small N
    • N has upper limit N_k
  • idea
    • 
  • no predefined converter for this formula
  • replace MultPower3Converter by CapacityConverter using Modelica code
    • block CapacityConverter
         extends SystemDynamics.Interfaces.GenericConverter3;
      equation
         out1 = in2/(1 - in1/in3);
      end CapacityConverter;
  • create new component
    • in OpenModelica: File/New/New Modelica Class
    • Name: CapacityConverter
    • Extends: SystemDynamics.Interfaces.GenericConverter3
    • Insert in class: SystemDynamicsExamples.AuxComponents
  • set N_k = 225
  • result
    • similar to previous version
    • 
  • "curve fits data" does not imply "model mechanism is correct"!