Algorithmen

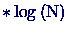Einen wesentlichen Einfluß auf das Laufzeit-Verhalten hat natürlich der verwendete Algorithmus; man denke z.B. nur an den Unterschied zwischen normaler und ''Fast'' Fourier-Transformation (N$*$N gegen N $*\log{(\mbox{N})}$ bei N Gitterpunkten). Zwar wird man einen Algorithmus auch nach den Kriterien der Genauigkeit und der numerischen Stabilität beurteilen müssen, man sollte aber den Geschwindigkeits-Aspekt immer berücksichtigen. Dies wird allerdings dadurch erschwert, daß die Rechner-Architektur zusätzlich eine Rolle spielt. Es gibt zum Beispiel Algorithmen, die theoretisch sehr schnell sind, aber trotzdem nicht eingesetzt werden, weil sie nicht vektorisieren.
Im Beispiel-Programm linalg werden zur Lösung eines linearen Gleichungssystems und zur Invertierung einer Matrix zwei verschiedene Algorithmen verwendet: Gauss-Jordan mit vollständiger Pivot-Suche und LU-Zerlegung mit partieller Pivot-Suche. Der oben angestellte Rechenzeit-Vergleich zeigt, daß die LU-Zerlegung deutlich schneller ist, erst recht, wenn man die Veclib-Routinen benutzt. Dies hat mehrere Ursachen: Zum einen ist vollständige Pivot-Suche sehr langsam und verhindert gutes Vektorisieren. Da partielle Pivot-Suche fast genauso stabil ist, wird man i. d. R. darauf zurückgreifen. Zum zweiten ist die LU-Zerlegung bei einer rechten Seite nicht langsamer als Gauss-Jordan, bei vielen Gleichungen aber schneller: Man muß nur einmal zerlegen und kann dann mit der Rücksubstitution sehr schnell viele rechte Seiten auswerten. Da auch sonst nichts für das Gauss-Jordan-Verfahren spricht, wird es heute nicht mehr eingesetzt, es ist auch in den gängigen Libraries (NAG, IMSL, Veclib) nicht enthalten.
Als weiteres Beispiel betrachten wir die Routinen GETVEC bzw. GETMAT. Sie besetzen einen Vektor bzw. eine Matrix mit gleichverteilten Zufalls-Zahlen zwischen -1 und 1. Bisher wurde dazu die Standard-Routine DRAND benutzt, die jeweils einen Wert zurückgibt. Die entsprechenden Schleifen können daher nicht vektorisiert werden. Die Veclib-Routine RANV dagegen gibt einen ganzen Vektor von gleichverteilten Zufallszahlen auf einmal zurück; außerdem ist sie der Convex-Architektur optimal angepaßt. Ohne genauere Kenntnis der jeweils verwendeten Algorithmen läßt sich über die Güte der Zufallszahlen von RANV bzw. DRAND nichts sagen, für unsere einfachen Zwecke sind aber beide sicher gleichwertig. In Version 2.5 sind GETVEC und GETMAT entsprechend geändert. Mit dem CXpa erhält man für die CPU-Zeiten incl. aufgerufener Unterroutinen folgende Ergebnisse:

Routine	CPU-Zeit		CPU-Zeit		.	Zeitersparnis		.
	DRAND		RANV		.	[%]		.
								.
getmat	0	.	028	1	.	020m	96	.	4
getvec	0	.	879m	0	.	020m	97	.	7