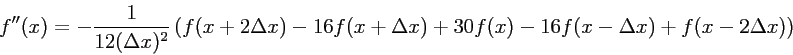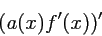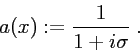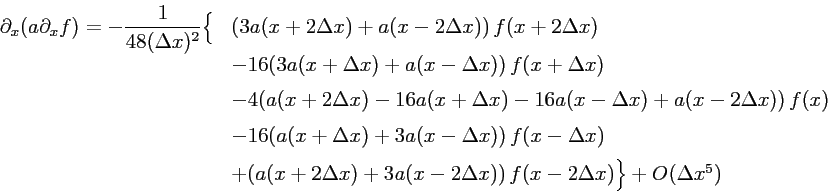Implementation - Nothing is simple

• Finite differences:
  • numerical solution based on DeRaedt's algorithm
  • starting point: discrete version of ∂_x² to 4^th order
    • 
  • PML-enhanced Schrödinger equation → discrete version of
    • 
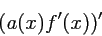
    • where
    • 
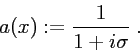
  • one possible solution
    • 
  • how can one find it?
  • general ansatz containing 25 terms
    • symmetry Δx → -Δx ⇒ 13 terms
    • expand it into a taylor series and compare to the desired result (MuPad)
    • → singular linear system for the coefficients
  • systematical scan of its solution space with Matlab →
    • 43 formulae with 13 terms
    • 15 formulae with 12 terms
    • no shorter ones
• Performance considerations:
  • problems
    • complicated formula
    • coefficients a(x+nΔx) are depending on x - bad for DeRaedt algorithm
    • number of grid points has to be enlarged, typically by factor 2
  • first implementation: 22x slower than non-PML version
  • hard work
    • extensive caching of intermediate results
    • fast library for submatrix computations
    • optimisation of memory accesses
  • result: 3.3x faster
    • 6.5x slower than non-PML version
    • factor 2 already due to larger grid