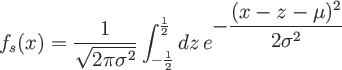Smoothing the distribution

• Approximation of N_g(μ, σ²):
  • discrete distribution cumbersome for large values (≙ high precision)
  • idea
    • approximate N_g with a continuous distribution N_s ("smoothed" normal)
    • interprete rounding as a special noise
  • concrete model
    • X_g = X + Y
    • where
    • X ∼ N(μ, σ²)
    • X_g = round(X)
  • Y interpreted as noise with
    • Y ∼ U(−0.5, 0.5)
    • useful approach in computer arithmetic
  • of course X, Y not independent!
• Experiment 3:
  • create random values X and X_g
  • compute Y = X - X_g
  • test Y ∼ U(−0.5, 0.5) with χ² test →

    • N	p-value
      3000	0.6165
      30000	0.5279

  • compute correlation coefficient ρ(X,Y) →

    • N	ρ
      3000	-0.0077
      30000	0.0085
      300000	0.0003

    • small, tends to 0 for large N (seemingly)
• Approximate probability density function f_s:
  • assume X, Y independent
    • → computation of density function easy via convolution
    • 
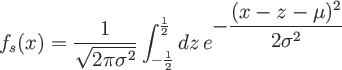
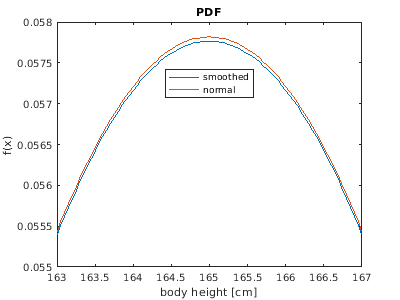
  • Gaussian smoothed over interval 1
  • coincides with exact discrete distribution at integer x
  • f_s and corresponding cdf F_s easily computed numerically
  • for standard values used here
    • 
• Experiment 4:
  • χ² testing using f_s
    • create rounded values as before
    • use edges on integral boundaries → test is sensitive to rounding
    • use F_s instead of Φ
  • results

    • N	p-value, Φ	p-value, Fs
      3000	0.0044	0.0046
      30000	3.7098e-42	4.9609e-42

  • idea completely useless!