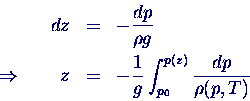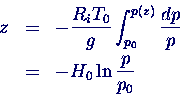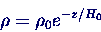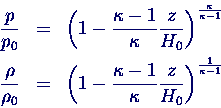Aerostatik

gesucht: Änderung des Drucks p mit der Höhe z
Grundbeziehung aus Kräftegleichgewicht wie oben
- dp = - ρ g dz
ρ nicht konstant
- von Druck und Temperatur abhängig
- ideale Gasgleichung verknüpft p, ρ, T
- p = ρ R_i T
- eine weitere Beziehung nötig
i.a auch g nicht konstant
- nimmt mit der Höhe ab
- grundsätzlich leicht zu berücksichtigen
- wird hier nicht weiter betrachtet
Integration liefert formal
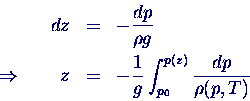
- mit Druck p₀ am Boden (bei z = 0)

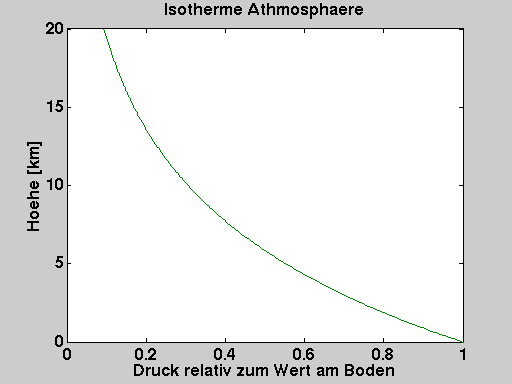
Isotherme Athmosphäre:
- Ansatz: Temperatur T = T₀ = konstant
- aus Gasgleichung daher
- Integration liefert
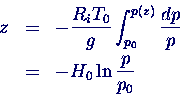
  - mit H₀ := R_i T₀/g
- Auflösen nach p ergibt
- damit für die Dichte
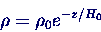
  - mit ρ₀ = p₀/(R_i T₀)
- graphisch
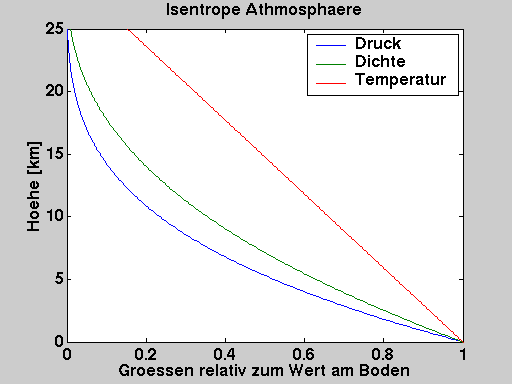
Isentrope Athmosphäre:
- Annahme: vertikaler Lufttransport ist adiabatisch
- Zusammenhang zwischen p und ρ
  - p/ρ^κ = const. (Adiabatengleichung)
- Integration und Auflösen nach p liefert dann
- Temperatur folgt aus der Gasgleichung zu
- Temperatur nimmt linear mit der Höhe ab
- Abnahme bei Standardbedingungen p₀ = 1013 mbar, T₀ = 15 °C
  - dT/dz = - 10 K/km
- graphisch
Polytrope Athmosphäre:
- statt Adiabate Polytrope mit Exponent n
- Beziehungen wie bei Adiabate mit κ → n
- daher Zusammenhang zwischen Temperaturabnahme und n
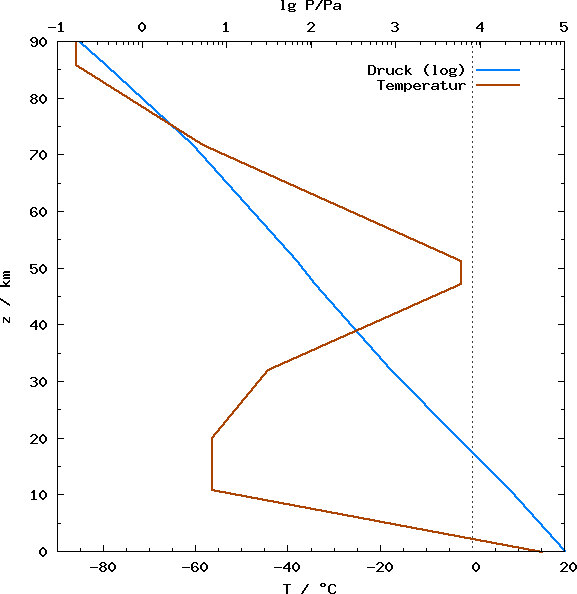
Erdathmosphäre:
- komplizierte Schichtung aufgrund von
  - Sonneneinstrahlung
  - Erdtopographie und -bodenbeschaffenheit
  - chemischen Prozessen
- Troposphäre
  - bis ca. 11 km
  - näherungsweise polytrop mit dT/dz = -6.5 K/km (n = 1.235)
  - instabil (warme Luft unten)
  - Bereich des Wetters
- Stratosphäre
  - bis etwa 47 km
  - zunächst T = const., dann Zunahme
  - chemische Prozesse durch UV-Licht der Sonne (Ozon-Schicht)
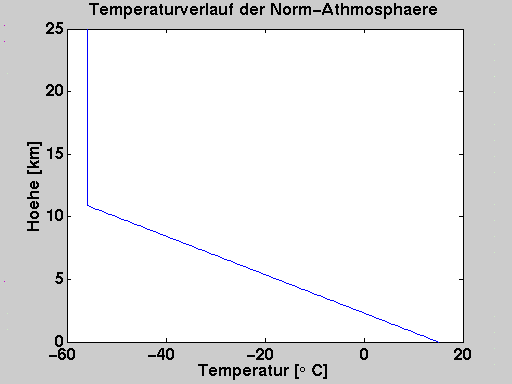
Standard-Athmosphäre:
- Basis für Berechnungen in Luft- und Raumfahrt
- Werte am Boden
  - p₀ = 1013.25 mbar
  - T₀ = 15 °C
  - ρ₀ = 1.225 kg/m³
- Temperaturverlauf
  - bis 11 km polytrop mit n = 1.235
  - darüber bis 25 km isotherm mit T = -56.5 °C
Aufgaben:
- Aufgabe 14