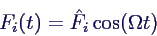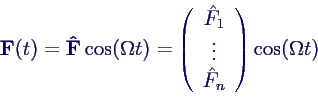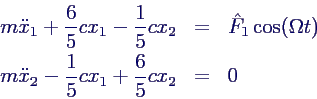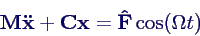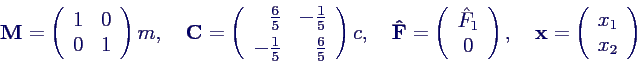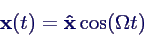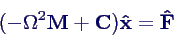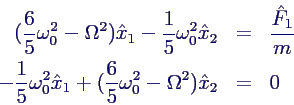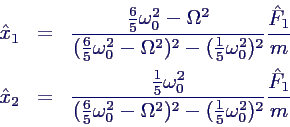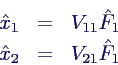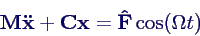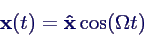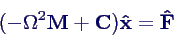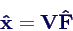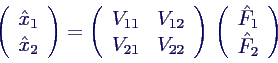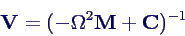Ungedämpfte Systeme

• Erregungskräfte bei gekoppelten Systemen:
  • Ursachen wie im 1d-Fall, z.B.
    • direkte Kraftübertragung
    • Fußpunkterregung
    • Unwuchten
    • Kombination mehrerer Fälle
  • Angriffspunkte z.B.
    • nur ein Schwinger (z.B. bei Fußpunkterregung)
    • mehrere Schwinger mit verschiedenen Ursachen
    • alle Schwinger in gleichmäßiger Weise
  • Zeitverhalten
    • gleichfrequente Erregung
    • harmonische Erregung
    • harmonische Erregung mit verschiedenen Frequenzen
    • unharmonische, aber periodische Erregung
    • unperiodische Erregung (z.B.Stoß)
    • Kombinationen
  • betrachten zunächst nur gleichmäßige harmonische Kraftübertragung
    • Kraft auf Masse m_i
    • 
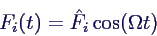
    • als Vektor geschrieben
    • 
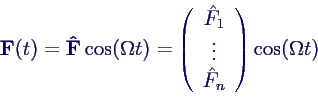
    • zusätzlicher Faktor Ω² in 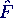_i bei Unwucht- oder Fußpunkterregung
    • Spezialfall eines Angriffspunkt: alle 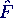_i = 0 bis auf einen
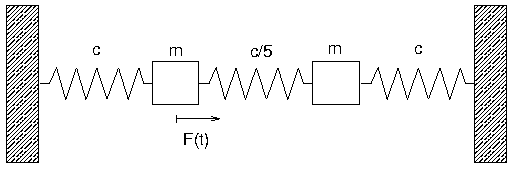
• Standardbeispiel mit Anregung:
  • Kraft nur auf 1. Masse
    
  • Bewegungsgleichungen
    • 
  • in Matrixform
    • 
  • mit
    • 
  • Lösung wieder Summe aus Lösung der homogenen Gleichung (Einschwingen) und partikulärer Lösung (Dauerschwingung)
• Berechnung der Dauerschwingung:
  • Ansatz
    • 
  • keine Dämpfung →
    • Phasenverschiebung 0 oder π
    • wird durch Vorzeichen von 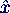_i berücksichtigt
  • Einsetzen in Bewegungsgleichung →
    • 
  • bzw. in Komponenten (mit ω₀² = c/m)
    • 
  • inhomogenes lineares Gleichungssystem, direkt auflösen →
    • 
• Analyse des Ergebnisses:
  • Amplitude der Kraft kann wie im eindimensionalen Fall abgespalten werden
    • 
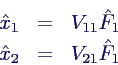
    • mit Vergrößerungsfunktionen V₁₁, V₂₁
  • Polynom im Nenner = charakteristisches Polynom der homogenen Gleichung →
    • Nullstellen sind gerade die Eigenfrequenzen ω_1,2
    • unendliche Amplitude bei den Eigenfrequenzen
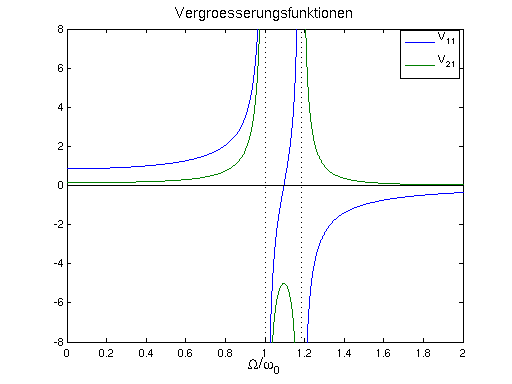
  • graphische Darstellung der Vergrößerungsfunktionen (mit ω₀ = 1)
    
  • Nullstelle von V₁₁ bei Ω ≈ 1.1 ω₀ →
    • Masse 1 ist in Ruhe (obwohl sie erregt wird)
    • sämtliche Energie geht in Schwingung der zweiten Masse
    • wichtige Methode zur Vermeidung von Schwingungen der Masse 1 (Schwingungstilgung)
• Allgemeines Vorgehen:
  • Aufstellen der Bewegungsgleichungen in Matrixform
    • 
  • Ansatz
    • 
  • liefert lineares Gleichungssystem
    • 
  • Auflösen nach 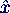→ fertig
  • Kraftkomponenten lassen sich abspalten
    • 
  • etwa im 2d-Fall
    • 
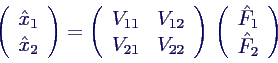
    • mit der Frequenzgang-Matrix V
  • lässt sich formal (oder bei nicht zu großen Systemen auch numerisch) leicht lösen
    • 
• Aufgaben:
  • Aufgabe 10
  • Aufgabe 11
  • Aufgabe 12