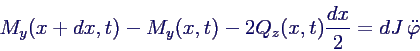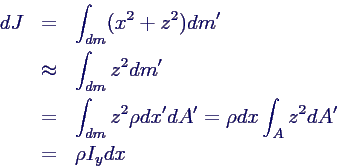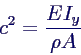Schwingungsgleichung des Balkens

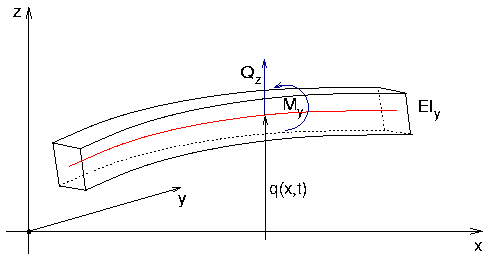
• Balken nach Bernoulli:
  • langer schmaler Körper mit konstantem Querschnitt
  • Verbiegung beschrieben durch Position q(x, t) des Flächenschwerpunkts (neutrale Faser)
    
    • schubstarr (keine Schubverformung)
    • nur in der x-z-Ebene
  • zwei Schwingungsformen
    • transversale Verschiebung mit q
    • Verbiegung mit q'
  • Zusammenhang zwischen Verbiegung und Biegemoment M_y
    • 
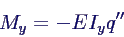
    • Elastizitätsmodul E
    • axiales Flächenträgheitsmoment I_y
• Herleitung der Schwingungsgleichung:
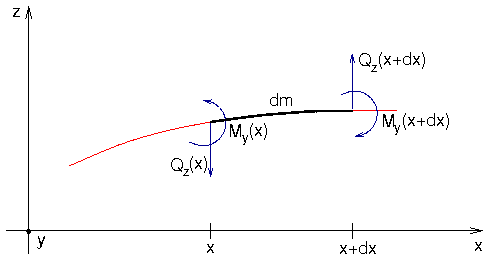
  • Kräfte bei Freischneiden von Massenelement dm
    
  • Kräftegleichgewicht für dm
    • 
  • für kleines dx also
    • 
  • Momentengleichgewicht für dm, bezogen auf den Mittelpunkt und den Winkel φ gegen die gerade Ausgangslage
    • 
  • dm ist sehr flache Scheibe, Fläche A, Dicke dx →
    • 
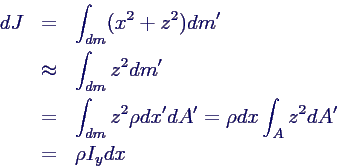
    • mit dem Flächenträgheitsmoment I_y
  • damit wird aus der Momentengleichung für kleines dx
    • 
  • rechte Seite
    • Trägheit bei Verbiegungsschwingung q'
    • häufig klein gegen Trägheit bei Verschiebung q
    • Näherung i.f.: Term ist 0 (Bernoulli-Balken)
    • genauere Berücksichtigung möglich (Timoshenko-Balken)
  • damit mit einmaligem Ableiten nach x
    • 
  • Zusammenhang zwischen M_y und q'' liefert dann
    • 
  • mit der Abkürzung
    •