Measuring the Performance of a Parallel Computer

• I measured the time it takes to solve a system of 6000 unknowns on our parallel computer. Measurements where taken for different numbers of processors, five runs each, since the times vary a little bit. Now we want to find out how we can describe the data.

• First we load the results from a file:

      load -ascii times.dat
      times
     
     times =
     
         1.0000   93.9700   96.0300   96.7500  121.2200   94.7300
         2.0000   51.5800   59.3100   49.7800   55.2400   60.3900
         4.0000   31.3100   38.1000   36.5600   31.6100   31.7400
         6.0000   29.0100   34.8100   32.9200   27.5900   28.4300
         8.0000   23.5300   21.4400   26.3600   27.6700   20.1000
        12.0000   21.0600   18.9100   25.4700   18.7300   19.9300
        16.0000   18.4400   21.2200   20.1200   20.3900   20.0400

• For convenience, we strip of the first column, containing the number of cpus:

      ncpus = times(:,1)
     
     ncpus =
     
          1
          2
          4
          6
          8
         12
         16

• And we collect the timing results in another array, with series in columns:

      timings = times(:, 2:end)'
     
     timings =
     
        93.9700   51.5800   31.3100   29.0100   23.5300   21.0600   18.4400
        96.0300   59.3100   38.1000   34.8100   21.4400   18.9100   21.2200
        96.7500   49.7800   36.5600   32.9200   26.3600   25.4700   20.1200
       121.2200   55.2400   31.6100   27.5900   27.6700   18.7300   20.3900
        94.7300   60.3900   31.7400   28.4300   20.1000   19.9300   20.0400  

• Now we compute the mean values of the measurement series:

      means = sum(timings)/size(timings,1)
     
     means =
     
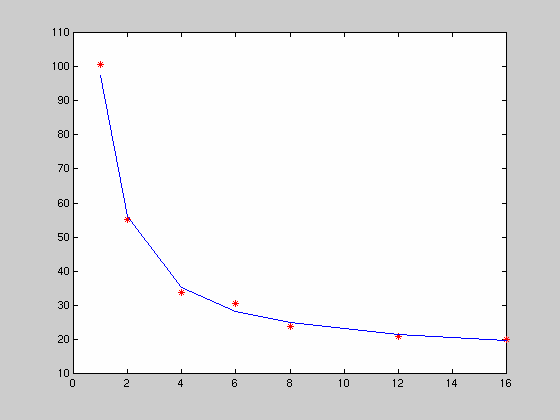
      100.5400   55.2600   33.8640   30.5520   23.8200   20.8200   20.0420

• Matlab already has some simple statistical functions, which work on columns of matrices:

      means = mean(timings)               
     
     means =
     
       100.5400   55.2600   33.8640   30.5520   23.8200   20.8200   20.0420
     
      devs = std(timings)
     
     devs =
     
       11.6113    4.6447    3.2143    3.1382    3.1961    2.7608    1.0101

• We want to fit the results to Amdahls law, which estimates the time T to run a program on N cpus as
  
  $$T(n) = T_s + 1/n T_p \hbox{\hspace{1cm}}\hbox{\hspace{1cm}}\hbox{\hspace{1cm}}(1)$$
  
  
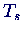  where $T_s$ is the time for the skalar part, which only runs on one cpu, and 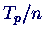$T_p/n$ the time for the parallel part that is n times faster on n cpus.

• To use the Matlab function polyfit, which fits data to a polynomial, we transform equation (1) into a polynomial (a linear function, in fact):
  
  $$S(n) := n*T(n) = T_s*n + T_p$$
  
  
  We transform our measured times in the array means accordingly:

      S = ncpus .* means'
     
     S =
     
       100.5400
       110.5200
       135.4560
       183.3120
       190.5600
       249.8400
       320.6720

• Now we fit S(n) to a linear function:

      coeff = polyfit(ncpus, S, 1)
     
     coeff =
     
       14.4960   82.9423

• These are the coefficients of the linear term and the constant term respectively, i.e we have
  
  $$T_s = 14.4960, T_p = 82.9423$$
  
  
  The fitted values are given by

      T_fit = coeff(1) + coeff(2) ./ ncpus
     
     
     T_fit =
     
        97.4383
        55.9671
        35.2316
        28.3197
        24.8638
        21.4079
        19.6799

• Finally we plot the measured values and the fit:

      plot(ncpus, means', 'r*', ncpus, T_fit)