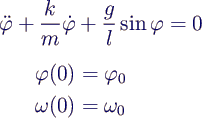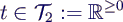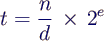Kontinuierliche Zeit

• Beispiel:
  • Bewegung eines mathematischen Pendels
  • interessierende Größen
    • Auslenkung φ(t)
    • Winkelgeschwindigkeit ω(t)
  • Beschreibung
    • Erdbeschleunigung g
    • Fadenlänge l
    • Dämpfungskonstante k
    • 
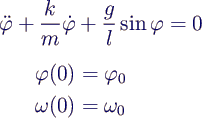
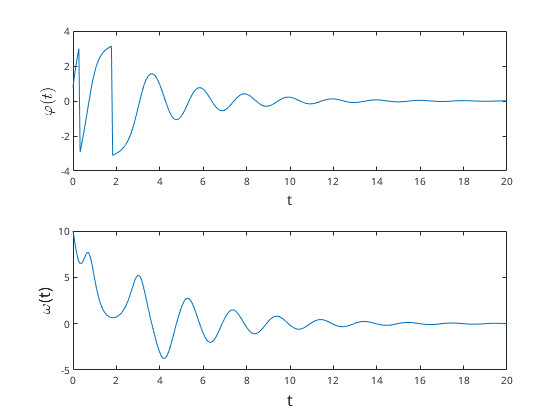
  •  typische Trajektorie
    
    • 
• Modellierung der Zeit:
  • Zeitwerte
    • 
  • mathematisch anspruchsvolles Modell!
    • Konstruktion von ℝ z.B. als Äquivalenzklassen von Folgen rationaler Zahlen
    • vielfältige Eigenschaften (Körper, Ordnung, Vollständigkeit)
  • für Anwender kein Problem
    • Existenz wird geglaubt
    • Eigenschaften sind vertraut
• Simulation:
  • ODE-Solver mit variabler Schrittweite → diskrete Zeitwerte im Computer
  • Alternative: Diskretisierung der Ergebniswerte
    
    • vgl. Riemann-Integral ↔ Lebesgue-Integral
    • entsprechende Solver (QSS = Quantized State System) intrinsisch zeitdiskret
  • Werte im Rechner sind Fließkommawerte 𝔽ℙ →
    
    • Beweisbarkeit von Eigenschaften schwer bei 𝔽ℙ als Modell
    • Gleichheit zweier berechneter Werte nicht gesichert
    • Reihenfolge zweier berechneter Werte nicht gesichert
  • sicherere Datentypen durch Einsatz ganzer Zahlen
    
    •  𝕀 ⊂ ℤ: Menge der Werte vom Datentyp Integer
    • damit z. B. t ≙ (n, d, e) mit n, d, e ∊ 𝕀 mit
    • 
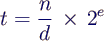
  • Problem bleibt auch bei allen folgenden Modellen