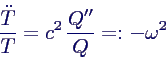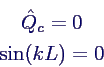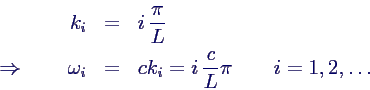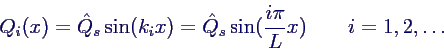Lösungen der Wellengleichung

• Laufende Wellen:
  • harmonische nach rechts laufende Welle
    • 
  • Einsetzen in Wellengleichung →
    • 
  • Wellen mit Ausbreitungsgeschwindigkeit c
  • allgemeine Lösung
    • 
  • beliebig geformte nach rechts und links laufende Wellen
• Stehende Wellen:
  • stationäre Schwingungsform entlang des Stabs
    
  • Überlagerung von sich gegeneinander bewegenden Wellen
  • z.B. durch Reflexion an den Enden
  • technisch bedeutsam wegen entsprechender Randbedingungen
• Beschreibung stehender Wellen:
  • Trennung von Raum- und Zeitanteil mit Produktansatz (Bernoulli)
    • 
  • Einsetzen in Wellengleichung →
    • 
  • ω hängt weder von t noch von x ab
  • Lösung der Gleichung für T
    • 
  • Amplitude steckt in Q
  • Lösung der Gleichung für Q
    • 
  • mit
    • 
  • Parameter ω, β, _c, _s aus Anfangs- und Randbedingungen
• Randbedingungen:
  • Forderungen für die Enden (des Stabs, der Saite etc.)
  • einfachste Form: explizite Bedingungen

    	Rand fest	keine Auslenkung	q = 0
    	Rand frei	keine Kräfte	q' = 0

  • Kräfte
    • z.B. beim Zugstab
    • F = E A q'
    • allgemein F ∼ q'
  • implizite Randbedingungen
    • Kräfte und Massen am Rand vorgegeben
    • z.B. bei elastischer Einspannung
    • ergibt Beziehung zwischen q und q' am Rand
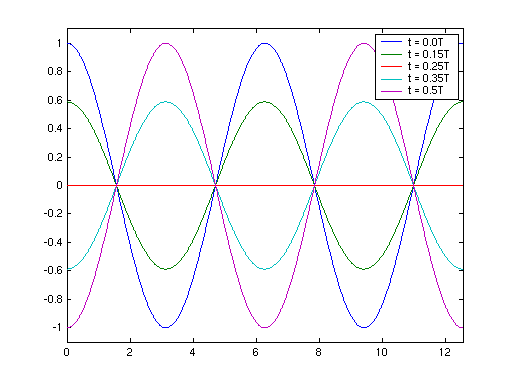
• Eigenschwingungen:
  • Beispielfall: Stab eingespannt bei x = 0 und bei x = L
  • Randbedingungen
    • q(0,t) = 0, q(L,t) = 0
  • gelten für alle Zeiten →
    • Q(0) = 0, Q(L) = 0
  • in Lösung für Q(x) einsetzen →
    • 
  • daraus ergeben sich unendlich viele Eigenfrequenzen
    • 
  • in Q(X) einsetzen → Eigenschwingungen
    • 
  • analog für andere Randbedingungen
• Aufgaben:
  • Aufgabe 17
  • Aufgabe 18